After reading recent articles by Hillel Wayne and Jordan Scales, I’ve become fascinated with the J programming language. Trying to learn J has opened my mind to new ways of thinking about code.

One of the things I find most interesting about J is its ties to natural language, and its corresponding use of code constructs called “hooks” and “forks”.

Many people argue that J is a “write-only” language because of its extreme terseness and complexity of syntax. As a beginner, I’d tend to agree, but I’m starting to warm up to the idea that it might be more readable than it first lets on.

What is J?

Other developers far more knowledgable than I have written fantastic introductions to the J programming language. I highly recommend you check out Hillel Wayne’s posts on hand writing programs in J and calculating burn rates in J. Also check out Jordan Scales’ posts on computing the Fibonacci numbers and Pascal’s triangle in J.

If you’re still not inspired, check out this motivating talk on design patterns vs anti-patterns in APL by Aaron Hsu, and watch Tracy Harms wax poetic about the mind-expanding power of consistency and adjacency in the J programming language.

Next be sure to check out the J Primer, J for C Programmers, and Learning J if you’re eager to dive into the nuts and bolts of the language.

If you’re only interested in a simple “TL;DR” explanation of J, just know that it’s a high-level, array-oriented programming language that follows in the footsteps of the APL programming language.

Language and J

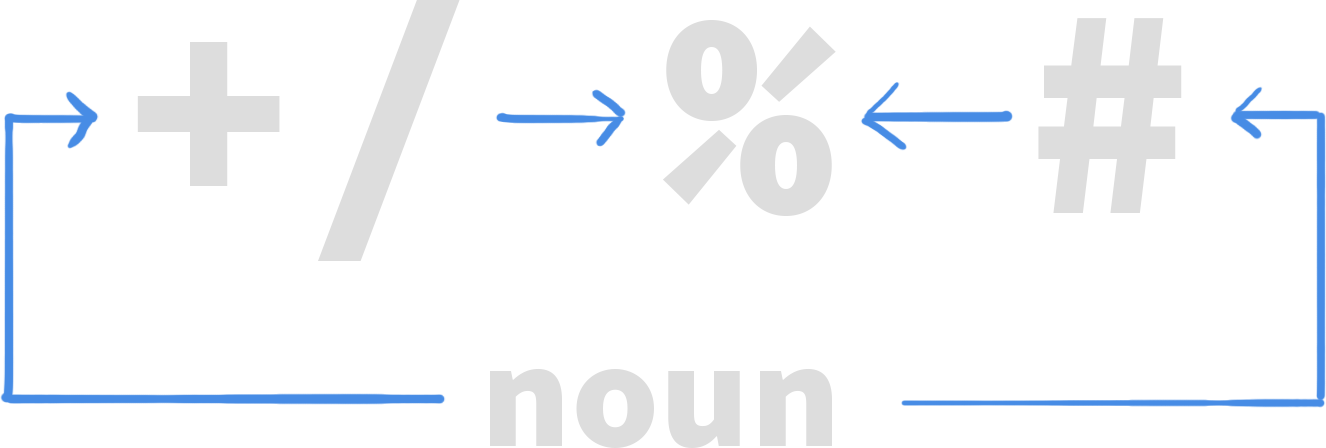
One of the most interesting aspects of J is that each component of a J expression is associated with a grammatical part of speech.

For example, plain expressions of data like the number five (5), or the list of one through three (1 2 3) are described as nouns. The “plus” operator (+) is a verb because it describes an action that can be applied to a noun. Similarly, the “insert” or “table” modifier (/) is an adverb because it modifies the behavior of a verb.

Unlike the human languages I’m used to, J expressions are evaluated from right to left. The following expression is evaulated as “the result of three plus two, multiplied by five”:

   5 * 2 + 3
25

We can modify our + verb with our / adverb to create a new verb that we’ll call “add inserted between”, or more easily, “sum”:

   +/ 1 2 3
6

Interestingly, all J verbs can easily operate over different dimensions (or ranks) of data. The + verb will happily and intuitively (in most cases) work on everything from a single atom of data to a many-dimensioned behemoth of a matrix.

Hooks and Forks

In J, any string of two concurrent verbs is called a “hook”, and any string of three concurrent verbs is called a “fork”. Hooks and forks are used to reduce repetition and improve the readability of our code.

Let’s look at a fork:

   mean =: +/ % #

Here we’re defining mean to be a verb composed of the “sum” (+/), “divided by” (%), and “tally” (#) verbs. This grouping of three verbs creates a fork.

When you pass a single argument into a fork, the two outer verbs (+/ and # in this case) both operate on that argument, and both results are passed as arguments to the middle verb. The resulting value of applying this middle verb is the final result of the fork expression.

A monadic fork applied to a noun.

Let’s use our mean verb to average the numbers one through four:

   mean 1 2 3 4
2.5

Just as we’d expect, the average of 1 2 3 4 is 2.5.

---

Now let’s try our hand at writing a hook. The routing of arguments within a monadic hook are slightly different than our mondaic fork. Let’s consider this example:

   append_length =: , #

Here we’re defining an append_length verb that first applies “length” (#) to append_length’s argument, and then applies “append” (,) to append_length’s original argument and the result of applying the “length” verb.

A monadic hook applied to a noun.

All that is to say that append_length is a hook that calculates that length of the provided argument and appends it to the end of that argument:

   append_length 0
0 1
   append_length append_length 0
0 1 2

I highly recommend checking out the guide on forks, hooks, and compound adverbs for a more complete explaination and overview of all of the hook and fork forms available to you as a J programmer.

I find myself producing lots of ranging content from books and articles, like the one you're reading now, to open source software projects. If you like what I'm doing, nothing shows your support more than signing up for my mailing list.

Speaking with Forks

On first exposure, the application rules for hooks and forks struck me as confusing and disorienting. I found myself asking, “why can’t they just stick to the right to left evaulation order?” My eyes were opened to the expressive power of forks when I stumbled across this gem of a quote in Jordan Scales’ article on computing the Fibonacci numbers in J:

[Forks] help us read out our expressions like sentences. For instance, “the sum times the last” can be written as +/ * {:, and our argument is automatically passed to both sides as it needs to be.

Let that sink in. I’ll be the first to admit that the argument routing built into J’s fork and hook constructs isn’t immediately obvious or intuitive, but that low level obfuscation leads to a higher level of clarity. We can read our forks like English sentences.

Let’s try it out with our mean verb:

   mean =: +/ % #

Here we’re saying that mean “is” (=:) the “sum” (+/) “divided by” (%) the “tally” (#).

We can even apply that idea to more complex J expressions, like this tacit expression from Hillel Wayne’s article on hand writing programs in J:

   tacit =: (?@:$ #) { ]

Without context, this expression would have initially overwhelmed me. But armed with our new tools about parsing and reading hooks and forks, let’s see if we can tease some meaning out of it.

Let’s look at the expression in parentheses first. It’s actually a hook of two verbs, ?@:$ and #. Using a little J-foo, we can recognize the first verb as being “shape of random” (?@:$), and the second verb is “tally” (#) , or “indices” in this context. Put together, the expression in parentheses is a verb that creates a “shape of random indices.”

All together, the tacit expression is a fork that reads, tacit “is” (=:) “shape of random indices” ((?@:$ #)) “from” ({) “the right argument” (]).

With arguments, this becomes a little more concrete. We want “a 3 4 shape of random indices from 'aaab'”.

   (3 4) tacit 'aaab'

And that’s just what we get:

abaa
aaab
abbb

Our tacit expressions has constructed a 3 4 matrix filled with random values from the 'aaab' string.

Hooked on Hooks and Forks

I’m far from being an expert in J. To be honest, I’m not even sure I’d call myself a beginner. The truth is that J is a very hard language to learn. Despite its difficultly (or maybe because of it?), I’m enamored with the language.

That said, I’m not going to go out tomorrow and start writing all of my production projects in J. In fact, I don’t imagine ever writing any production code in J.

J may not give me any concrete tools that I can use in my day-to-day work as a software developer, but it’s teaching me new ways of approaching old problems. In a field where constant growth is required and expected, this is an invaluable gift.